Wpływ długości trzpienia pomiarowego na błędy pomiarów wykonywanych na maszynach współrzędnościowych

Cechą charakterystyczną współczesnego przemysłu jest produkcja masowa, stopniowo wypierana przez masową customizację, czyli dopasowywanie produktu do indywidualnych potrzeb klienta [11]. Za jej symboliczny początek wiele źródeł przyjmuje datę 1 grudnia 1913 r. – dzień rozpoczęcia montażu taśmowego Forda T w zakładach Highland Park w Detroit.

Wydarzenie to było źródłem znacznych zmian w gospodarce, przyspieszyło w sposób znaczący postęp techniczny i w konsekwencji zmusiło przedsiębiorców do wykonywania przedmiotów zgodnie z określonymi, wcześniej założonymi standardami. Równolegle z rozwojem technik wytwarzania nastąpił rozwój metod pomiarowych. Stosowane w tamtym okresie urządzenia optomechaniczne realizowały proste zadania pomiarowe oraz posiadały ograniczoną dokładność pomiaru [6]. Ciągłe doskonalenie metod wytwarzania w szczególności rozwój maszyn NC, a następnie CNC spowodowała zapotrzebowanie na szybsze i bardziej elastyczne środki pomiarowe.

Pierwszą współrzędnościową maszyną pomiarową było urządzenie opracowane przez szkocką firmę Ferranti w 1959 roku. Maszyna ta służyła jedynie do pomiaru w dwóch osiach. Trzecią oś w roku 1963 wprowadziła włoska firma DEA [22,23].

Rozwój tych urządzeń spowodował powstanie wielu odmian konstrukcyjnych, które zostały opisane w wielu pozycjach literaturowych [21,24-31].

 

Współrzędnościowa technika pomiarowa

Współrzędnościowa technika pomiarowa (WTP) stanowi stosunkowo nowy obszar metrologii wielkości geometrycznych. Pomiary realizowane są z użyciem urządzeń nazywanych zbiorczo współrzędnościowymi systemami pomiarowymi (CMS ang.). Zaliczamy do nich współrzędnościowe maszyny pomiarowe (WMP) które zwykle wykonują pomiar w trójwymiarowym układzie kartezjańskim zgodnie z ich konstrukcją, ale także urządzenia, które nie posiadają prostoliniowych osi ruchu, w układzie niekartezjańskim takie jak ramiona pomiarowe.

WMP to obecnie najbardziej wszechstronne, a jednocześnie precyzyjne przyrządy pomiarowe. Mogą one wykonywać pomiary elementów o dużym stopniu złożoności i komplikacji oraz wysokich wymaganiach dokładnościowych w relatywnie krótkim czasie. Cechy te umożliwiają dostosowanie do nawet bardzo dynamicznych cykli produkcyjnych oraz w sposób istotny wpływać na jakość procesów wytwarzania. Cechują się bardzo wysoką elastycznością, co przy częstych zmianach konstrukcyjnych i technologicznych spotykanych we współczesnym przemyśle (szczególnie motoryzacyjnym) jest niewątpliwą zaletą [1,3,17].

 

Trzpienie pomiarowe i ich układy oraz zastosowanie

Budowę trzpienia pomiarowego przedstawiono na rysunku 1. Zgodnie z definicją normy ISO 10360-1 składa się on z końcówki trzpienia pomiarowego i trzonu [15]. Stanowi niezbędne wyposażenie do przeprowadzenia pomiarów stykowych na współrzędnościowej maszynie pomiarowej. Końcówka trzpienia pomiarowego podczas pracy ma fizyczny kontakt z elementem mierzonym i odpowiedzialna za prawidłowe przeniesienie geometrii zmierzonej, poprzez układ głowicy pomiarowej do pamięci komputera. Trzpień jest mocowany bezpośrednio w głowicy pomiarowej lub za pomocą talerzyka pomiarowego samodzielnie, lub z użyciem przedłużaczy, łączników, rozgałęzień, elementów obrotowych itp.

 

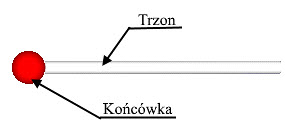
Rys. 1. Budowa trzpienia pomiarowego

 

Trzpienie dobieramy w zależności od zadania pomiarowego zwracając uwagę na ich maksymalną sztywność oraz jak największą dokładność geometryczną. W tym celu niezbędna jest odpowiednia praktyka oraz doświadczenie ze względu na dużą różnorodność zarówno typów jak i materiałów czy producentów.

 

Błędy pomiarów współrzędnościowych

Wykonanie pomiaru absolutnego nie jest (zgodnie z obecnym stanem wiedzy) możliwe, dlatego nie możemy określić wartości wielkości mierzonej eliminując wszystkie błędy. Szczególnie podczas pomiarów stykowych w technikach współrzędnościowych, kiedy końcówka pomiarowa ma fizyczny kontakt z przedmiotem mierzonym wtedy sam proces pomiaru powoduje powstawanie zakłóceń (rys. 2).

 

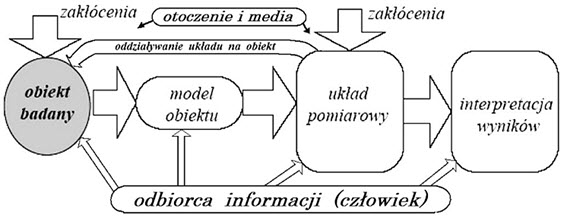
Rys. 2. Powiązania pomiędzy elementami procesu pomiarowego [9]

 

Błędy wpływające na wynik pomiaru można zmniejszyć, zwiększając nakłady kosztów i pracy zmniejszyć, lecz nigdy nie można ich całkowicie wyeliminować [7,9,12,13].

 

Błędy maszyn współrzędnościowych

We współrzędnościowej technice pomiarowej istotnymi czynnikami mającymi wpływ na końcowy wynik pomiaru są błędy pomiarowe oraz ich źródła. Źródłami nie jest jedynie maszyna pomiarowa, lecz także inne wpływające na wynik czynniki (rys.3) które dzielimy na pięć podstawowych grup i do których zaliczamy: maszynę pomiarową, środowisko (otoczenie), operatora (czynnik ludzki), metodę pomiarową, przedmiot badany [4,5,7,10].

 

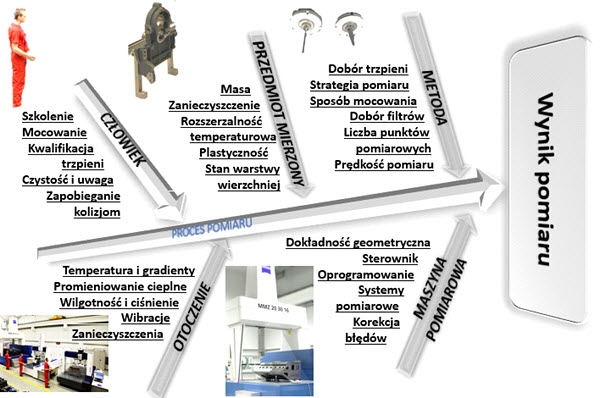
Rys. 3. Źródła błędów technice współrzędnościowej (opr. własne)

 

Do błędów związanych z maszyną należą: błąd pomiaru długości E_L, oraz rozrzut powtarzalności błędu pomiaru długości R₀.

Parametr R_0, oznacza rozstęp powtórzonych trzykrotnie pomiarów długości przeprowadzonych na WMP przy zastosowaniu trzpienia o długości offsetu równej zero. Wartość graniczną błędu wyznacza parametr R_0, MPL, czyli granica dopuszczalna maksymalna rozstępu powtarzalności [16]. W celu wyznaczenia R₀ wykonujemy serię trzech powtórzeń pomiarów każdego z badanych wymiarów (minimum 35 pomiarów), z których wyników obliczamy wartość rozstępu. Aby system przyjąć jako zgodny ekstremalne wartości powtarzalności muszą być niższe lub równe wartości R_{0, MPL} założonej przez producenta lub przyjętej przez użytkownika.

 

Stanowisko pomiarowe i przedmiot badań

Badania przeprowadzono na portalowej współrzędnościowej maszynie pomiarowej Zeiss MMZ M (rys. 4), przeznaczonej do pomiaru dużych i dokładnych części takich jak: korpusy maszyn, duże koła zębate, elementy silników okrętowych i elektrowni wiatrowych. Maszyna posiada zabezpieczone osłonami wszystkie prowadnice i inne istotne elementy konstrukcyjne dzięki czemu może pracować zarówno bezpośrednio na hali produkcyjnej w zanieczyszczonej atmosferze, a także w specjalnie wydzielonych klimatyzowanych pomieszczeniach. Konstrukcja maszyny oparty jest o korpusy stalowe spawane i została zoptymalizowana pod kątem sztywności oraz odporności na zmiany temperatury. Żeliwny stół pomiarowy jest niezależnie od WMP osadzony w bloku fundamentowym [2].

 

Rys. 4. Współrzędnościowa maszyna pomiarowa Zeiss MMZ M 30 60 20 (opr. własne)

 

Przedmiot badań (rys. 5) stanowił jednowymiarowy certyfikowany wzorzec długości maksymalnej 500 mm. Powierzchnie pomiarowe wzorca wykonane w postaci wałeczków ceramicznych o równoległych płaszczyznach czół umożliwiają pomiar 25 wymiarów liniowych.

 

Rys. 5. Stopniowy wzorzec długości (opr. własne)

 

Niepewność pomiaru wzorca długości określona jest wzorem:

 

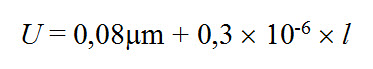
Tabela 1. Długości pomiarowe wzorca wykorzystane w badaniu (opr. własne)

Numer powierzchni pomiarowej	Odległość od powierzchni pomiarowej 0 [mm]
1	20,00078
7	140,00399
13	259,94510
19	379,93024
25	499,96299

 

Do badań nad wpływem długości trzpienia na parametry E₀ oraz R₀, na WMP MMZ M zastosowano dziesięć układów trzpieni pomiarowych z końcówkami kulistymi. Składały się one z trzpieni lub trzpieni i przedłużek, których parametry przedstawiono w tabeli 2. Po zamocowaniu trzpienia w talerzyku typu VAST i umieszczeniu go w głowicy pomiarowej przeprowadzono kwalifikację układu trzpieni. Nacisk pomiarowy generowany przez głowicę podczas badań dla wszystkich układów to 200 mN

 

Tabela 2. Parametry trzpieni pomiarowych [20,32]

L.p.	Gwint	DK [mm]	L [mm]	ML [mm]	DS [mm]	DG [mm]	Masa [g]	Materiał trzonu	Materiał kulki
MasterProbe – trzpień referencyjny
1	M5	8	63	50	6	-	28	węglik wolframu	rubin syntetyczny
L75
2	M5	8	75	62	6	-	30	węglik wolframu	rubin syntetyczny
L115
3	M5	8	114,5	101,5	6	-	49	węglik wolframu	azotek krzemu
L160
4	M5	10	165	150	6	11	52	węglik wolframu	azotek krzemu
L200
5	M5	8	200	186	4	11	87	węglik wolframu	azotek krzemu
L250
6	M5	8	250	230	6	11	108	węglik wolframu	azotek krzemu
L350
7	M5	10	345	332	6	11	120	węglik wolframu	rubin
L450
8.1	M5	8	250	230	6	11	108	węglik wolframu	azotek krzemu
8.2		20	200	Przedłużka			85	aluminium
L550
9.1	M5	10	345	332	6	11	120	węglik wolframu	rubin
9.2		20	200	Przedłużka			85	aluminium
L750
10.1	M5	8	250	230	6	11	108	węglik wolframu	azotek krzemu
10.2		20	500	Przedłużka			89	thermofit
L1000
11.1	M5	8	114,5	101,5	6	-	49	węglik wolframu	azotek krzemu
11.2		20	400	Przedłużka			75	thermofit
11.3		20	500				89

 

Maksymalna masa całkowita dla trzpienia L1000 wyniosła 371g.

Dla głowicy VAST G2 dopuszczalna masa układu trzpieni wynosi 600 g, a maksymalna zalecana przez producenta długość układu trzpieni to 800 mm.

 

Badanie błędu E_{0, MPE} oraz rozstępu powtarzalności R_{0, MPE} dla różnych długości trzpieni pomiarowych

Zgodnie z zaleceniami normy dla E₀ offset trzpienia pomiarowego względem pinoli musi wynosić zero lub być możliwie najmniejszą wartością do badań wykorzystano trzpień referencyjny którego offset równy jest zeru.

Wzór matematyczny definiujący dopuszczalny błąd graniczny współrzędnościowej maszyny pomiarowej podczas pomiaru wymiaru określony w normie ISO 10360-1 E, _MPE może być przedstawiony w trzech postaciach:

a) MPEE = ± minimum z (A + L / K) i B (Rys. 7.2a) [15],
b) MPEE = ± (A + L / K) (Rys. 7.2b) [15],
c) MPEE = ± B (Rys. 7.2c) [15].

Stałe określone we wzorach:

A - podawana przez producenta stała dodatnia, wyrażona w mikrometrach;
K - podawana przez producenta stała dodatnia bezwymiarowa;
L - jest mierzoną długością, wyrażoną w milimetrach;
B - błąd graniczny dopuszczalny MPE_E, w mikrometrach, ustalony przez producenta.

 

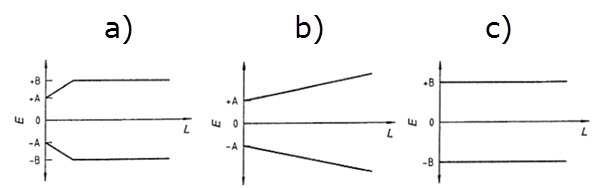
Rys. 6. Błędy graniczne dopuszczalne wskazania CMM podczas pomiaru wymiaru [15]

 

Producent badanej maszyny podaje wzór zgodnie z rysunkiem 6b dlatego do obliczeń i analizy przyjęto jego postać zgodnie normą:

 

MPE_E = ± (A + L / K).

 

Metodyka badań

Cykl pomiarowy [8] podczas sprawdzania błędu E, _MPE składał się z następujących kroków:

1. Czynności przygotowania CMM do pracy.
2. Wyznaczenie położenia kuli wzorcowej w celu wykonania cykli kwalifikacji trzpieni. Kula wzorcowa ceramiczna o średnicy 30mm przymocowana została do stołu CMM. Położenie kuli wzorcowej definiuje się z użyciem specjalnego trzpienia referencyjnego zwanego „MasterProbe”.
3. Przygotowanie (montaż) trzpienia w celu jego kwalifikacji.
4. Kwalifikacja trzpienia pomiarowego – czynność mająca na celu sprawdzenie jego parametrów i określenie położenia w stosunku do trzpienia referencyjnego (wyznaczenie offsetu trzpienia). W przypadku maszyn Zeiss offsetem zerowym jest punkt wyznaczony w środku końcówki kulistej trzpienia referencyjnego.
5. Zamocowanie wzorca. Mocowanie umożliwia prawidłowe i powtarzalne zorientowanie mierzonego elementu w przestrzeni maszyny pomiarowej.
6. Pomiar wymiarów wzorcowych w celu wyznaczenia błędu E_MPE. Pomiar został przeprowadzony w cyklu CNC z orientowaniem ręcznym dla pierwszego przebiegu (w celu ustalenia położenia wzorca w przestrzeni maszyny pomiarowej). Program pomiarowy składał się z trzykrotnego pomiaru pięciu wybranych wymiarów liniowych. Podczas pomiaru aktywowano opcję korekcji temperatury części mierzonej z użyciem układu CMM.
7. Zmiana położenia wzorca (odpowiednio w osiach X, Y, Z) ponowienie pomiaru zgodnie z pkt. 6.
8. Po zakończeniu dla danego trzpienia cyklu pomiarowego następuje jego zmiana i proces powtarza się od punktu 3 do 7.

W wyniku przeprowadzonych badań dotyczących wpływu długości trzpienia uzyskano 1350 wyników pomiaru długości, które poddano analizie.

 

Wyniki badań

Badania rozpoczęto od sprawdzenia parametrów E_{0, MPE} oraz R_{0, MPE} z użyciem trzpienia referencyjnego. Wyniki tych badań miały potwierdzić przydatność urządzenia do przeprowadzania badań oraz stanowić wynik referencyjny dla późniejszych czynności. Wyniósł on 0,9 µm dla osi X oraz 0,4 µm dla osi Y, co spełnia założenia producenta (R₀ =1,8 µm). Następnie sprawdzono błąd E_{0, MPE} określany przez producenta na poziomie +/-3,2 µm + L/400 (rys.7). Ze względu na zbyt krótki offset trzpienia i brak możliwości pomiaru nie sprawdzono E_{0, MPE} dla osi Z.

 

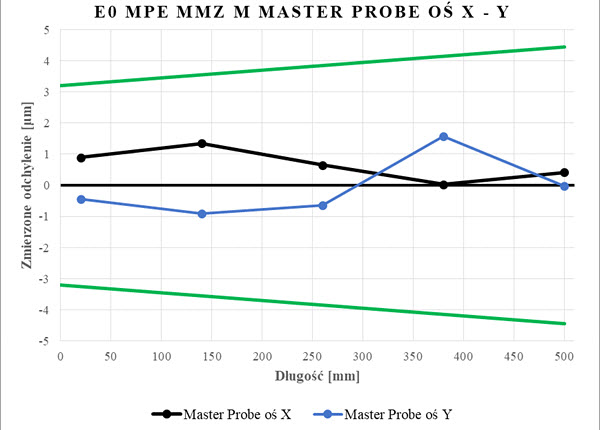
Rys. 7. Wykres wyników pomiaru błędu E_{0, MPE} [32]

 

Wyniki rozrzutu uzyskane podczas kwalifikacji poszczególnych trzpieni przedstawiono na rysunku 8. Odchyłkę kwalifikacji określa odchylenie standardowe obliczone podczas pomiaru punktów na kuli wzorcowej. Jest ono obliczane na podstawie zmierzonych wartości promienia końcówki kulistej trzpienia pomiarowego. Dla trzpieni o długości L75 oraz L115 kwalifikacja przebiegała tylko w orientacji równoległej do osi Z, ze względu na zbyt mały offset uniemożliwiający przeprowadzenia pomiaru liniału w osi pionowej (XY na wykresie). Dla pozostałych trzpieni kwalifikacja przeprowadzana była dwukrotnie – dla orientacji pionowej trzpienia (XY na wykresie) oraz równoległej (Z). Wyniki kwalifikacji przyjmowane jako pozytywne to odchylenie standardowe kwalifikacji trzpienia poniżej 0,5 µm dla trzpieni od długości do 500 mm. Dla trzpieni powyżej 500 mm za pozytywny wynik kwalifikacji przyjmowana jest wartość odchylenia standardowego poniżej 0,2 µm. Jak wynika to z przedstawionych na wykresie danych (rys. 8) wyniki kwalifikacji były pozytywne dla każdej z długości trzpienia. Widoczne wyraźnie są dwa trendy – zwiększanie się wartości zmierzonej odchylenia standardowego wraz ze wzrostem długości trzpienia oraz wyraźnie większe jego wartości dla orientacji poziomej trzpienia w stosunku do położenia pionowego. Maksymalna różnica pomiędzy orientacją pionową i poziomą wynosiła 50% dla trzpienia o długości 550 mm. Różnica pomiędzy odchyłką kwalifikacji najdłuższego i najkrótszego trzpienia wynosi 1 µm dla orientacji pionowej i 1,2 µm dla orientacji poziomej.

 

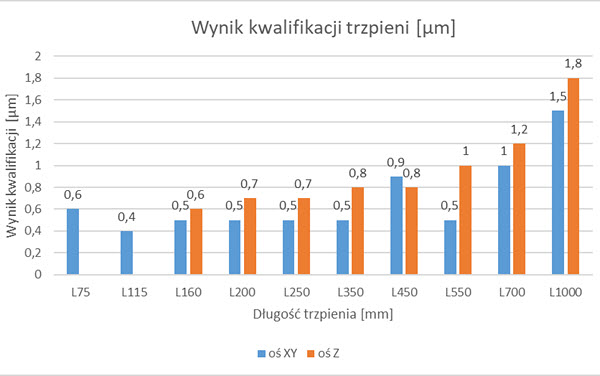
Rys. 8. Wyniki kwalifikacji trzpieni wykorzystanych w badaniach [32]

 

W następnym kroku z uzyskanych danych obliczono błąd R₀ dla poszczególnych długości trzpieni (rys. 9).

Uzyskane wyniki mieszczą się w tolerancji założonej przez producenta. Najmniejszą wartość rozstępu powtarzalności odnotowano dla zestawu L200; R₀=0,0003 mm, najwyższą dla zestawu L1000 – 0,0017 mm. Rozkład wyników jest równomierny, z tendencją wzrostu rozrzutu wraz ze wzrostem długości trzpieni. Widoczny jest trend dla układów w osi Z – dla większości długości trzpienia uzyskana wartość jest mniejsza niż analogiczna w osiach X czy Y. Na rysunkach 9 do 19, przedstawiono wyniku pomiaru błędu E_{L, MPE}, dla wszystkich użytych układów trzpieni.

 

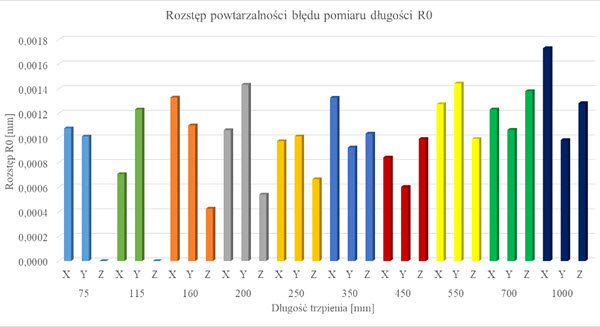
Rys. 9. Wykres wartości R₀ dla różnej długości trzpieni badanych na WMP Zeiss MMZ M [32]

 

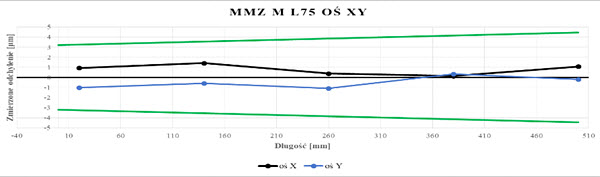
Rys. 10. Wykres wartości E_L dla układu trzpieni L75 badanego na WMP Zeiss MMZ M (opr. własne)

 

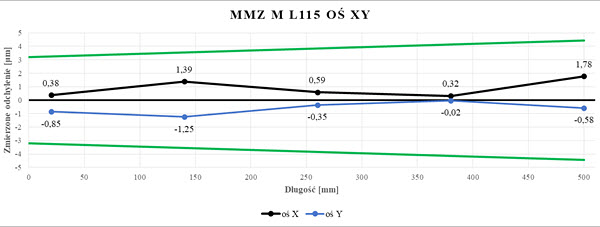
Rys. 11. Wykres wartości E_L dla układu trzpieni L115 badanego na WMP Zeiss MMZ M (opr. własne)

 

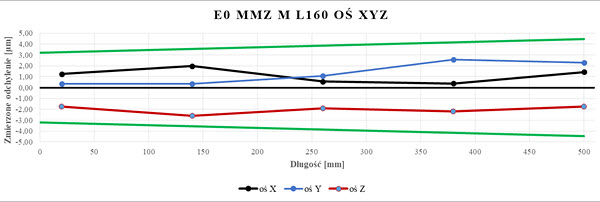
Rys. 12. Wykres wartości E_L dla układu trzpieni L160 badanego na WMP Zeiss MMZ M (opr. własne)

 

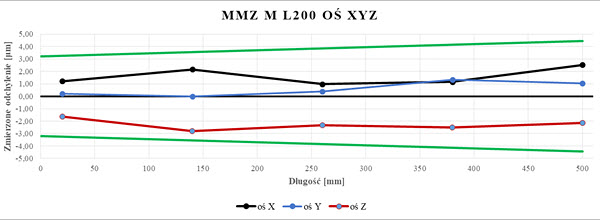
Rys. 13. Wykres wartości E_L dla układu trzpieni L200 badanego na WMP Zeiss MMZ M (opr. własne)

 

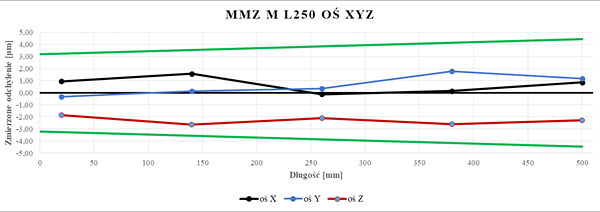
Rys. 14. Wykres wartości E_L dla układu trzpieni L250 badanego na WMP Zeiss MMZ M (opr. własne)

 

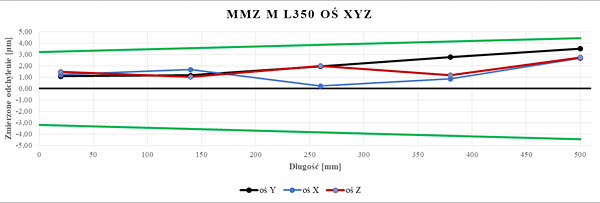
Rys. 15. Wykres wartości E_L dla układu trzpieni L350 badanego na WMP Zeiss MMZ M (opr. własne)

 

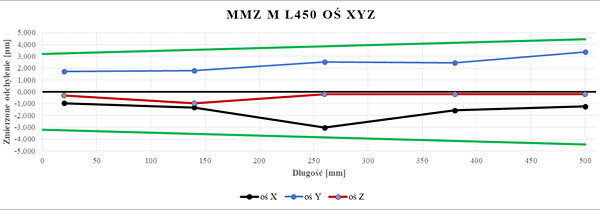
Rys. 16. Wykres wartości E_L dla układu trzpieni L450 badanego na WMP Zeiss MMZ M (opr. własne)

 

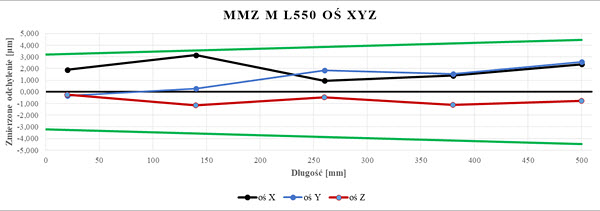
Rys. 17. Wykres wartości E_L dla układu trzpieni L550 badanego na WMP Zeiss MMZ M (opr. własne)

 

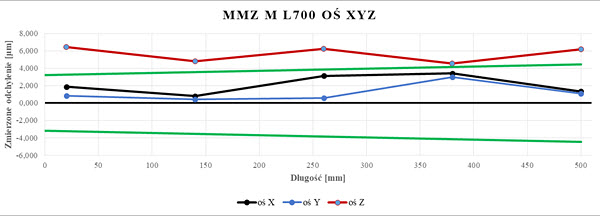
Rys. 18. Wykres wartości E_L dla układu trzpieni L700 badanego na WMP Zeiss MMZ M (opr. własne)

 

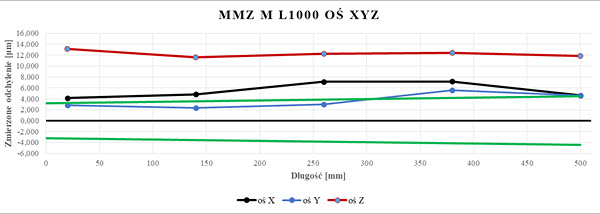
Rys. 19. Wykres wartości E_L dla układu trzpieni L1000 badanego na WMP Zeiss MMZ M (opr. własne)

 

Analiza wyników badań

W celu przeprowadzenia analizy wyników wpływu długości trzpienia na parametr E_{L, MPE} przy danej długości offsetu trzpienia względem głowicy L trzpienie oznaczono jako:

a) L75 – wielkość offsetu 11 mm,
b) L115 – wielkość offsetu 50 mm,
c) L160 – wielkość offsetu 95 mm,
d) L200 – wielkość offsetu 136,5 mm,
e) L250 – wielkość offsetu 186,5 mm,
f) L350 – wielkość offsetu 280,5 mm,
g) L450 – wielkość offsetu 336,5 mm,
h) L550 – wielkość offsetu 435,5 mm,
i) L750 – wielkość offsetu 680 mm,
j) L1000 – wielkość offsetu 935 mm.

Wyniki pomiarów zestawiono w formie tabel i wykresów(rys.20-22) dla poszczególnych długości trzpieni. Dane zawarte na wykresach opisano wcześnie, od pozycji L160 na wykresach pojawia dodatkowy wykres w kolorze brązowym reprezentujący wyniki dla błędów dopuszczalnych granicznych osi Z maszyny współrzędnościowej. Na podstawie wykonanych pomiarów ustalono, że wartości pomiarów dla trzpieni L75, L115, oraz L160 są niemal identyczne jak dla wartości zmierzonych trzpieniem referencyjnym. Wraz ze wzrostem długości trzpienia zmierzone odchylenia wartości nominalnych zwiększają się. Wyjątek stanowi pomiar osi X dla L450 gdzie wartości są niższe od nominału. Aż do L550 (długość offsetu 435 mm) wyniki dla wszystkich osi są w granicach wyznaczone tolerancji. Dla trzpienia o długości L700 wyniki pomiaru osi Z są negatywne – otrzymane rezultaty nie spełniają założonych wymagań, jednak wyniki osi X oraz Y pozostają w tolerancji choć widoczne jest ich przesunięcie do granicy wartości granicznych.

W przypadku trzpienia L1000 (offset 935 mm) jedynie wyniki osi Y w niepełnym zakresie znajdują się w granicach tolerancji. Pozostałe wyniki leżą po za tolerancją, w przypadku pomiaru osi Z dla wymaganej wartości wymiaru 20 wynoszącej 3,25 μm wartość zmierzona wyniosła 13,18 μm.

Ponadto w celu analizy kompleksowej wykonano trzy wykresy zbiorcze (rys. 20,21 oraz 22) dla wszystkich długości badanych trzpieni zawierające zmierzone odchylenia dla poszczególnych osi w postaci wykresów słupkowych. Granice pola tolerancji przedstawiono jako linie w kolorze czerwonym.

 

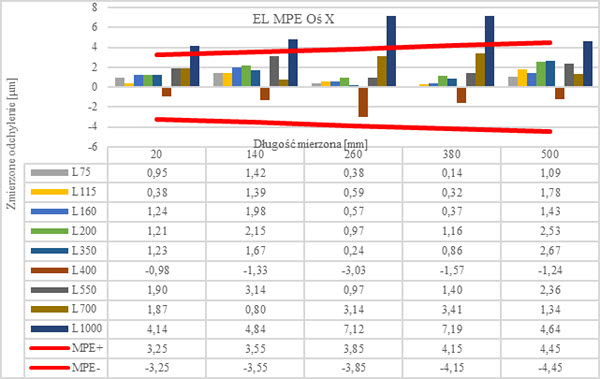
Rys. 20. Agregacja zmierzonych wartości E_L dla osi X (opr. własne)

 

Wyniki pomiaru w osi X przedstawione zostały na rysunku 20. Wykresy poszczególnych długości zostały uporządkowane pod względem wartości mierzonych na wzorcu długości. Widoczny jest wyraźny trend wzrostu błędu pomiaru wraz ze wzrostem długości trzpienia dla każdego mierzonego wymiaru (wyjątek stanowi wspomniany wcześniej trzpień o długości L400).

Brak jest widocznych tendencji do wzrostu błędu pomiaru wraz ze wzrostem wielkości mierzonego wymiaru. Rozkład wartości jest równomierny. Najniższe odchylenie od wartości nominalnej w osi X zmierzono dla długości 380 (wartość nominalna 379,93024 mm), wynosiło ono 0,14 μm dla trzpienia L75. Najwyższa wartość przekraczająca pole tolerancji E=7,19 μm dla trzpienia L1000 również dla wymiaru 380.

 

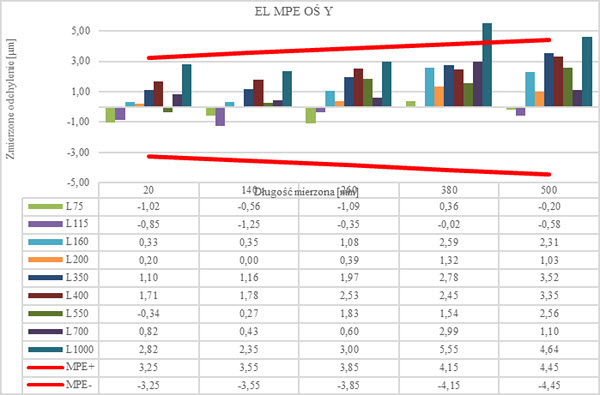
Rys. 21. Agregacja zmierzonych wartości E_L dla osi Y (opr. własne)

 

Rezultaty uzyskane podczas pomiarów przeprowadzonych w osi Y przedstawiono na rysunku 21. Podobnie jak dla osi X wyraźnie widoczny jest wzrost błędu pomiaru wraz ze wzrostem długości trzpienia dla każdego z mierzonych wymiarów (dotyczy wszystkich długości układów trzpieni).

Możemy zaobserwować tendencję do wzrostu błędu pomiaru dla wymiarów 380 oraz 500. Najniższe odchylenie E=0 μm w osi Y stwierdzono dla wymiaru 140 (wartość nominalna 140,00399 mm) i długości trzpienia pomiarowego L200. Trzpień ten ma wszystkie zmierzone wartości odchyleń najbardziej zbliżone do wartości nominalnych. Najwyższe odchylenie o wartości E=5,55 μm (przekroczenie wartości granicznej) zmierzono dla trzpienia L1000 i wymiaru L380 analogicznie jak w przypadku osi X.

 

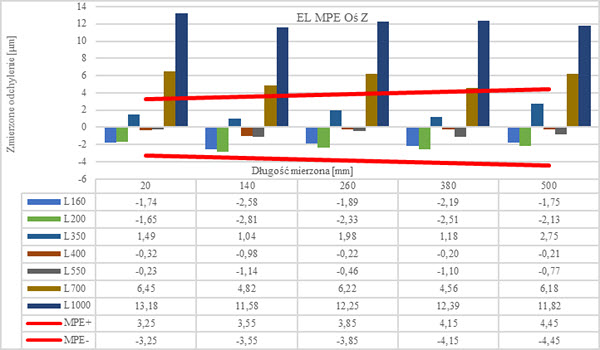
Rys. 22. Agregacja zmierzonych wartości E_L dla osi Z (opr. własne)

 

Pomiary w osi Z zestawiono na wykresie 22. Trend wzrostu błędu pomiaru wymiarów długościowych wraz ze wzrostem długości trzpienia dla każdej mierzonej pozycji pokrywa się z omówionymi wcześniej wynikami osi X oraz Y.

Nie obserwujemy tendencji wzrostowej dla błędu pomiaru wymiarów ich charakterystyka jest najbardziej równomierna ze wszystkich sprawdzanych osi. Najniższe odchylenie E=0,20 μm stwierdzono dla wymiaru 380 i trzpienia pomiarowego L400. Zmierzone wartości odchyleń najbardziej zbliżone do wartości nominalnych obserwujemy dla trzpieni L350, L400 oraz L550. Trzpienie L700 oraz L1000 mają najwyższe błędy pomiaru, przekraczające dopuszczalne wartości graniczne. Najwyższe odchylenie o wartości E=4,45 μm zaobserwowano dla trzpienia L1000 i wymiaru L500.

 

Wnioski z przeprowadzonych badań

Podczas badań nad wpływem długości zastosowanego trzpienia pomiarowego na wartość dopuszczalnego błędu granicznego współrzędnościowej maszyny pomiarowej MMZ M wykorzystano 10 różnych układów trzpieni. Użyte trzpienie i inne elementy układu trzpieni są podstawowymi i najczęściej spotykanymi w praktyce pomiarów współrzędnościowych. Badane zestawy cechuje celowy brak homogeniczności: użyto trzpieni o różnej długości, średnicy i materiale końcówki kulistej. Cechą wspólną wszystkich użytych trzpieni był materiał ich trzonów w postaci węglika wolframu. Cechuje go najlepsza sztywność co jest istotnym czynnikiem zmniejszającym błąd ugięcia trzpienia. Także materiały przedłużenia trzpieni są różnie (aluminium i włókno węglowe). Dla najdłuższych układów trzpieni L750 oraz L1000 użyto przedłużeń z włókien węglowych ze względu na ich niską masę i bardzo dobrą sztywność. Zastosowane długości układów trzpieni w przypadku jednego zestawu (L1000) przekraczając określoną przez producenta dopuszczalna długość układu trzpieni pomiarowych. Dobór taki miał na celu ocenę przydatności układu trzpieni o parametrach po za specyfikacją.

Uzyskane wyniki zbiorcze przedstawiono kolejno na rysunkach 23,24 oraz 25 odpowiednio dla osi maszyny pomiarowej X, Y, Z.

 

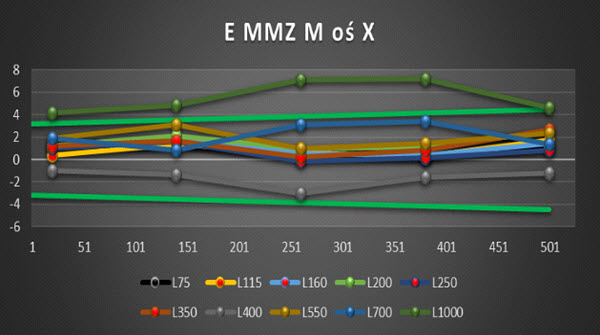
Rys. 23. Wykres wyników pomiaru dopuszczalnego błędu granicznego E, _MPE dla dziesięciu długości układu trzpieni w osi X (opr. własne)

 

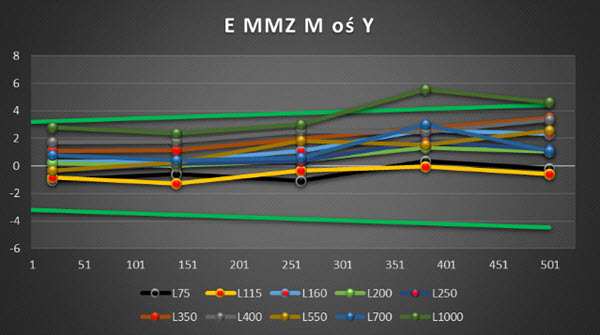
Rys. 24. Wykres wyników pomiaru dopuszczalnego błędu granicznego E, _MPE dla dziesięciu długości układu trzpieni w osi Y (opr. własne)

 

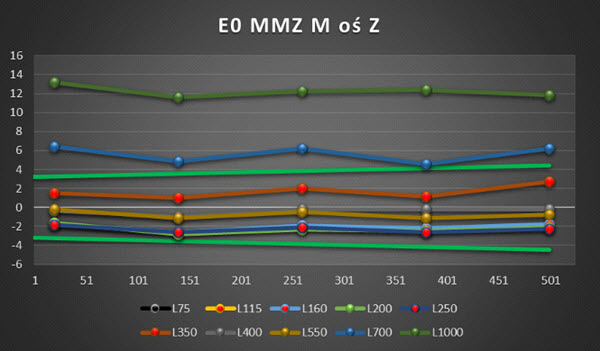
Rys. 25. Wykres wyników pomiaru dopuszczalnego błędu granicznego E, _MPE dla dziesięciu długości układu trzpieni w osi Z (opr. własne)

 

Analizując wykresy możemy wywnioskować, iż najdłuższa użyteczna długość z zastosowanych badaniach układów trzpieni to L700 (z wyjątkiem osi Z) co potwierdza specyfikację producenta. Trzpień o długości L1000 nie spełnia wymagań podczas żadnego z przeprowadzonych pomiarów. Widoczny brak istotnej tendencji do liniowego wzrostu błędu wraz ze zwiększaniem się długości trzpienia jest spowodowany specjalnym trybem kwalifikacji trzpienia dla maszyn pomiarowych Zeiss z głowicami Zeiss G2 i oprogramowaniem Calypso. Podczas kwalifikacji trzpieni w tzw. trybie „tensor”, CMM stosuje pomiar punktów na kuli wzorcowej z dwoma różnymi wartościami siły nacisku generowanymi przez głowicę. Dzięki takiemu zabiegowi oprogramowanie potrafi określić wartość ugięcia dla kwalifikowanego trzpienia i odpowiednio go skompensować.

 

Podsumowanie

Prawidłowy dobór trzpienia pomiarowego ma istotny wpływ na dokładność pomiarów współrzędnościowych. Na rynku dostępna jest szeroka oferta różnych producentów wybór więc może być problematyczny. Aby zoptymalizować układ trzpieni należy stosować kilka podstawowych zasad ich doboru:

- możliwie krótkiego trzpienia do realizacji danego zadania pomiarowego – minimalizuje to ewentualne ugięcie trzpienia,

- konstrukcja układu z jak najmniejszej ilości elementów – minimalizuje to ilość połączeń, z których każde jest potencjalnym źródłem błędów,

- dobór końcówki kulistej trzpienia o jak największej możliwej średnicy – końcówka kulista działa jako filtr mechaniczny ponadto zwiększony jest prześwit pomiędzy nią a trzonem trzpienia pomiarowego.

Ważną zasadą jest także przestrzeganie zaleceń producenta dotyczącą maksymalnej długości trzpienia i masy układów trzpieni. Dobrą praktyką jest również zakup dedykowanych trzpieni danego producenta możemy mieć wtedy pewność, że ich parametry są optymalnie dobrane do możliwości głowicy pomiarowej.

 

BIBILIOGRAFIA

1. Bosch J. A.: Coordinate Measuring Machines and Systems, CCRC Press, 1995.
2. Dokumentacja techniczno ruchowa CMM Zeiss MMZ M.
3. Dudziak M., Kołodziej A., Kroczak J., Podolski T.: Uncertainty Evaluation During Designing of Geometrical Form of Machines Elements, Machine Modeling and Symulations, pp. 21-28, 2009.
4. Glazowski P., Michalski R.: Wyznaczenie niepewności pomiaru CMM z użyciem niewykalibrowanego obiektu, Inżynieria Wytwarzania, Kalisz, Wydawnictwo PWSZ w Kaliszu, pp. 83-94, 2018.
5. Glazowski, P, Michalski R.: Wpływ błędu MPEE na dokładność pomiaru współrzędnościowej maszyny pomiarowej, Stal, pp. 49-52, 11-12 2019.
6. Gocał J.: Wybrane Technologie Pomiarów Inżynierskich Oparte Na Wykorzystaniu Instrumentów Elektronicznych, Prace Instytutu Geodezji I Kartografii Akademia Górniczo-Hutnicza, Kraków, tom 48, nr 102, pp. 88-106, 2001.
7. Gruca M., Grzelka J., Pyrc M., Szwaja S.: Miernictwo i systemy pomiarowe, Częstochowa, 2007.
8. Hopp G.: Schulungsunterlagen zu Calupso und Llage Schulung, AALEN: Carl Zeiss 3D akademie, 2006.
9. Humienny Z., Kiszka K.: Metrologia i zamienność, Warszawa: Skrypt Politechniki Warszawskiej, 2011.
10. Jakubiec W., Malinowski J.: Metrologia wielkosci geometrycznych, Warszawa: WNT, 1999.
11. Littler C.R.: Technology and the Organisation of Work, Victoria (Australia), Deakin University, 1991.
12. NPL Measurement Good Practice Guide No. 11: The Begginer's Guide to Uncertainty of Measurement, Teddington, Middlesex, UK: National Physical Laboratory, 2001.
13. NPL Measurement Good Practice Guide No. 41: CMM Measurement Startegies, Teddington, Middlesex, UK: National Physical Laboratory, 2001.
14. NPL Measurement Good Practice Guide No. 42: CMM Verification, Teddington, Middlesex, UK: National Physical Laboratory, 2001.
15. PN-EN ISO 10360-1 – wersja polska, Specyfikacje geometrii wyrobów (GPS) -- Badania odbiorcze i okresowe współrzędnościowych maszyn pomiarowych (CMM) - Część 1: Terminologia.
16. PN-EN ISO 10360-2 – wersja polska, Specyfikacje geometrii wyrobów (GPS) - Badania odbiorcze i okresowe współrzędnościowych maszyn pomiarowych (CMM) - Część 1: CMM stosowane do pomiaru wymiarów liniowych.
17. Ratajczyk E.: Tendencje w rozwoju współrzędnościowej techniki pomiarowej, Pomiary Automatyka, Kontrola, pp. 05-09, 12 2005.
18. Rothmeyer R.: Measurement Strategies in Tactile Coordinate Metrology, Aalen: Zeiss Metrology Academy, 2015.
19. Sładek J.: Dokładność pomiarów współrzędnościowych, Wydawnictwo PK, Kraków 2011.
20. http://www.zeiss.pl/industrial-metrology/, 20 Listopad 2019. [Online]
21. Marciniak – Podsadna L., Metodyka badania dokładności optycznych skanerów współrzędnościowych, Rozprawa Doktorska, Poznań 2013, str, 11 – 64.
22. Sładek J., Dokładność pomiarów współrzędnościowych, Wydawnictwo Politechnika Krakowska, Kraków 2011, str. 371 – 401.
23. Znaniecki P., Koncepcja systemu nadzorowania współrzędnościowych maszyn pomiarowych w warunkach produkcyjnych, Rozprawa Doktorska, Poznań, 2012.
24. Iwasińska O., Ratajczyk E., badanie dokładności maszyn hybrydowych na przykładzie współrzędnościowej maszyny pomiarowej ScanMax, IV Międzynarodowa Konferencja Naukowa – współrzędnościowa Technika Pomiarowa, Zeszyty Naukowe Politechniki Łódzkiej Fila Bielsko Biała nr 53 – Bielsko Biała 2000, str. 106 – 114.
25. Rupik J., Jendrollik J., Wieczorowski M., Wykorzystanie techniki współrzędnościowej do pomiaru precyzyjnych elementów wielkogabarytowych, Postęp w Metrologii Współrzędnościowej, Akademia Techniczno – Humanistyczna w Bielsku Białej, Bielsko – Biała, 2010, str. 115-124.
26. Weckenman A., Geus D., Gubesch A., High Precision form and dimension measurements with toctile measuring machines, IV Międzynarodowa Konferencja Naukowa Politechniki Łódzkiej Filia w Bielsku – Białej nr 53, 2000, str. 255 – 264.
27. Ratajczyk E., Nowe rodzaje współrzędnościowych maszyn pomiarowych i nowe oznaczenia ich parametrów. Część I: Parametry charakteryzujące dokładność, Mechanik nr 4, 2017, str. 324 – 327.
28. Ratajczyk E., New types of coordinate measuring machines and symbole used for their parameters, Part II: Examples of portal machines, Mechanik 5-6, 2017 str. 462 – 467.
29. Ratajczyk E., Tendencje w rozwoju współrzędnościowej techniki pomiarowej, Pomiary Automatyka Kontrola, nr 12, 2005, str. 5 – 9.
30. Ratajczyk E., Zaawansowane pomiary współrzędnościowe w technikach wytwarzania, Pomiary Automatyka Kontrola, vol. 53, nr 9bis, 2007, str. 9 - 16.
31. Nowa wersja Zeiss Contura – tak funkcjonalna jak maszyny pomiarowe wyższej klasy, Mechanik, nr 5 – 6, 2019, str. 382 – 383.
32. Glazowski P. „Wpływ długości trzpienia pomiarowego i jego zużycia na błędy pomiarów wykonanych techniką współrzędnościową”, Praca dyplomowa, Kalisz 2020.

 

mgr inż. Roman Michalski,
mgr inż. Przemysław Glazowski